Les surfaces infranchissables au "corpuscule" prétendu
Sommaire
- 1 Solutions explicites, pour l'atome d'hydrogène
- 2 Les objections de Michel Talon, 13 avr 2006, 11:06
- 3 Remise en discussion : le statut du pratiquement non observable, mais prédit par la théorie.
- 4 Reprise du débat, février 2009
- 5 L'expérience a tranché : les domaines de phase des orbitales sont observés
Solutions explicites, pour l'atome d'hydrogène
Nous allons ici étudier les solutions connues depuis 1926, de l'équation de Schrödinger, appliquées à l'atome le plus simple, l'hydrogène, et constater que dès que le nombre quantique principal est supérieur à 1, elles contiennent des surfaces à amplitude identiquement nulles, d'inversion de phase. Or qui dit densité identiquement nulle, dit que l'interprétation en "probabilité de présence" est aussi identiquement nulle ; ces surfaces, notamment sphériques, sont donc infranchissables au prétendu corpuscule qui serait sensé s'agiter entre zones de densité non nulle. Donc dès 1926, c'est la totalité de la communauté des physiciens, et non le seul Erwin Schrödinger, qui aurait dû jeter aux orties l'idéation corpusculaire.
Notations de W. Greiner
Erreur probable :
La source est le Pauling & Wilson, et il me semble que toutes les formules sont erronées. Remplacer les par des
?
Je relève aussi des discordances de polynômes de Laguerre selon les auteurs... A suivre.
| n | l | |
|
Sphères nulles | Plans nuls |
|---|---|---|---|---|---|
| 1 | 0 | |
|
0 | 0 |
| 2 | 0 | |
1 : |
0 | |
| 2 | 1 | |
|
0 | 1 |
| 3 | 0 | |
2 : |
0 | |
| 3 | 1 | |
1 : |
1 | |
| 3 | 2 | |
|
0 | 2 |
| 4 | 0 | |
3 | 0 | |
| 4 | 1 | |
2 | 1 | |
| 4 | 2 | |
1 | 2 | |
| 4 | 3 | |
|
0 | 3 |
| 5 | 0 | |
4 | 0 | |
| 5 | 1 | |
3 | 1 | |
| 5 | 2 | |
2 | 2 | |
| 5 | 3 | |
1 | 3 | |
| 5 | 4 | |
0 | 4 |
On constate que plus le nombre quantique principal est élevé, plus chaque électron est scindé entre zones distinctes, de phases deux à deux opposées.
Notations
a0 est le rayon de Bohr : où
est la masse réduite, proche de me :
.
Sources et bibliographie
Linus Pauling & E. Bright Wilson, Jr. Introduction to Quantum Mechanics, with Applications to Chemistry. Réed. Dover, 1985.
Wolfgang Greiner. Quantum Mechanics, an introduction. Springer Verlag, 1989.
P.W. Atkins. Molecular Quantum Mechanics. Oxford University Press, 1983.
Jean-Louis Basdevant. Mécanique Quantique. Ellipses, 1986.
E. V. Chpolski. Physique atomique. Tome 2. Fondements de la mécanique quantique et structure de l'enveloppe électronique de l'atome. Edition Mir, Moscou 1974, 1978 pour la traduction française.
Les objections de Michel Talon, 13 avr 2006, 11:06
Je me permets de revenir avec beaucoup de retard sur ce point qui me paraît intéressant. Il est vrai que dans le cas des solutions usuelles pour l'atome d'hydrogène on voit apparaître des surfaces où la probabilité de présence vaut 0 et qui séparent des régions où elle est comprise entre 0 et 1. Selon la manière dont on comprend philosophiquement le mouvement du "farfadet" entre ces régions on peut se poser des problèmes, mais je ne veux pas aborder ces problèmes qui par nature ne peuvent mener qu'à des discussions infinies.
Simplement je veux faire remarquer un point purement technique, que j'aurais du soulever bien plus tôt, et qui est qu'en général de telles surfaces où la probabilité de surface est nulle et qui séparent des domaines où elle est > 0 n'existent pas, du moins je le crois. Si je ne me trompe pas, ça enlève de la force à cette objection, dans le cas où on la prendrait dans un sens réaliste.
Pourquoi dis-je cela? L'atome d'hydrogène est un problème intégrable et en conséquence on peut appliquer une séparation des variables. En l'occurrence la position du "farfadet" est caractérisée par r, theta, phi et on cherche la fonction d'onde sous la forme f(r) g(theta) h(phi) et il se trouve que ça marche. La conséquence évidente est que là où f(r)=0, ce qui a des solutions r=r_i, la probabilité de présence est nulle pour tout theta phi, c'est à dire en fait sur une sphère. Les sphères r=r_i constituent des surfaces qui séparent topologiquement des régions où la probabilité de présence est >0. La même chose va se passer pour tous les systèmes intégrables où on peut séparer les variables d'une manière ou d'une autre. Mais en physique aucun système concret n'est intégrable! Par exemple déjà l'atome d'hélium isolé n'est pas un système intégrable, et même l'atome d'hydrogène ne le sera pas si on tient compte d'une interaction par exemple avec le rayonnement. Si le système n'est pas intégrable il n'y a plus aucune raison pour que le phénomène décrit ci-dessus se produise. Prenons le cas de l'atome d'hélium avec 2 électrons. la fonction d'onde est donc fonction non plus de 3 mais de 6 coordonnées. La condition d'annulation psi=0 donne une seule relation entre ces 6 coordonnées. Il reste 5 degrés de liberté arbitraires. Je ne vois pas en quoi ceci peut définir des surfaces de probabilité de présence nulle séparant des zones de probabilité de présence >0. De plus à ma connaissance les exemples de résolution numérique de telles équations ne montrent pas ce genre de phénomène.
En conséquence, même si l'on pensait que la probabilité de présence reflète en fait la fréquence de présence du "farfadet" se déplaçant à toute vitesse d'un endroit à l'autre (une interprétation de type statistique), et même si on pensait que cette interprétation interdit de traverser une zone de probabilité de présence nulle (ce qui n'est pas absolument clair quand il s'agit d'une zone qui est aussi de mesure nulle), je ne pense pas que l'objection tienne dés lors qu'on s'adresse à un système qui est un minimum réaliste, c'est à dire pas à un système intégrable.
--
Michel TALON
Jacques Lavau, 13 avr 2006, 14.00
Erreur de principe, et grossière : c'est que les zones de densité identiquement nulle, sont simplement les zones où l'onde électronique change de signe, passe par zéro. La continuité n'ayant pas changé, ces frontières peuvent avoir une géométrie plus compliquée, sans changer d'existence, ni même de topologie. Or la densité n'est que le carré hermitien de l'amplitude.
Voilà ce que c'est que d'avoir totalement perdu de vue les bases de la résolution de l'équation de Schrödinger, et dérivées.
Michel TALON, 13 avr 2006, 14.52
Jacques Lavau <Nolavauspamjac@klube_internaite.effaire> wrote:
> Erreur de principe, et grossière : c'est que les zones de densité
> identiquement nulle, sont simplement les zones où l'onde électronique
> change de signe, passe par zéro. La continuité n'ayant pas changé, ces
On est bien d'accord, je n'ai jamais dit le contraire.
> frontières peuvent avoir une géométrie plus compliquée, sans changer
> d'existence, ni même de topologie. Or la densité n'est que le carré
> hermitien de l'amplitude.
Oui mais elles peuvent avoir une géométrie telle qu'elles ne séparent plus l'espace en zone disjointes. C'est là tout le problème. Donc pour savoir ce qui se passe il n'y a qu'une solution, trouver quelque part sur le web une résolution de l'atome d'Hélium et voir si ça fait apparaître des zones comme on en voit pour l'atome d'hydrogène. Une chose est sûre c'est que la raison qui fait que ça se passe comme ça pour l'hydrogène n'existe plus pour l'hélium.
Or, et je répète et rééxplique mon argument, suppose qu'il existe une surface S de l'espace à 3 dimensions qui le sépare en 2 zones et telle que la probabilité de présence est nulle quand l'un des deux électrons est sur cette surface, quelle que soit la position de l'autre. Ca veut dire que la structure des zéros de la fonction d'onde psi(x_1,y_1,z_1,x_2,y_2,z_2) est trés particulière (je te rappelle que la fonction d'onde est fonction des 6 coordonnées des deux électrons). A priori il n'y a aucune raison pour que la solution de psi = 0 (où psi est une fonction plus ou moins analytique des x) soit de la forme (x_1,y_1,z_1) appartient à S, (x_2,y_2,z_2) quelconque ou le contraire. Ceci suppose une dégénérescence, une factorisation de psi qui ne peut pas se produire en général.
Au total je maintiens mon argument et je prétends que c'est toi qui doit réfléchir à la situation avant de parler des erreurs grossières des autres.
--
Michel TALON
Jacques Lavau, 13 avr 2006, 21.07
Michel Talon a écrit : Landau & Lifchitz, pp 299-300 Cohen-Tannoudji, Diu & Laloë, T2, complément A XIV, B XIV, pp 1404 - 1425. W. Greiner. Quantum Mechanics, Special chapters. chapitre 11. pp 285 - 329. n-l-1 représente toujours le nombre de noeuds dans la partie radiale de la fonction d'onde.
> Or, et je répète et rééxplique mon argument, suppose qu'il existe une surface
> S de l'espace à 3 dimensions qui le sépare en 2 zones et telle que la
> probabilité de présence est nulle quand l'un des deux électrons est sur cette
> surface, quelle que soit la position de l'autre.
Raisonnement circulaire : tu supposes préalablement des électrons corpusculaires "plus petits" que l'atome. Tantôt présents, tantôt absents, etc. etc. Elles sont où, les expériences qui soutiennent cette mystique ?
> Ca veut dire que la structure
> des zéros de la fonction d'onde psi(x_1,y_1,z_1,x_2,y_2,z_2) est trés
> particulière (je te rappelle que la fonction d'onde est fonction des 6
> coordonnées des deux électrons). A priori il n'y a aucune raison pour que
> la solution de psi = 0 (où psi est une fonction plus ou moins analytique des
> x) soit de la forme (x_1,y_1,z_1) appartient à S, (x_2,y_2,z_2) quelconque
> ou le contraire. Ceci suppose une dégénérescence, une factorisation de psi
> qui ne peut pas se produire en général.
La topologie ne subit aucun changement dans les levées de dégénérescences des fréquences et niveaux d'énergie. Seuls changent les rayons, la répartition azimuthale dans les Z élevés, et éventuellement des couplages r-azimuth qui déforment la symétrie sphérique vers une tétraèdrique, ou autre dans les molécules et les cristaux.
> Au total je maintiens mon argument et je prétends que c'est toi qui doit
> réfléchir à la situation avant de parler des erreurs grossières des autres.
Il s'agit toujours d'une erreur grossière, et pour soutenir une thèse toujours indéfendable.
Michel Talon, Jeu 13 avr 2006 21:38
Jacques Lavau <Nolavauspamjac@klube_internaite.effaire> wrote:
> Landau & Lifchitz, pp 299-300
> Cohen-Tannoudji, Diu & Laloë, T2, complément A XIV, B XIV, pp 1404 - 1425.
> W. Greiner. Quantum Mechanics, Special chapters. chapitre 11. pp 285 -
> 329.
> n-l-1 représente toujours le nombre de noeuds dans la partie radiale
> de la fonction d'onde.
Tu dis n'importe quoi, il n'y a pas de partie radiale pour un système à deux électrons, il n'y a aucun moyen de séparer un "rayon" dans le problème. Tout ce que tu as pu voir dans les livres porte sur un traîtement approximatif. Par exemple on traîte un système avec un électron en supposant que le deuxième donne un champ moyen.
> > Or, et je répète et rééxplique mon argument, suppose qu'il existe une surface
> > S de l'espace à 3 dimensions qui le sépare en 2 zones et telle que la
> > probabilité de présence est nulle quand l'un des deux électrons est sur cette
> > surface, quelle que soit la position de l'autre.
> Raisonnement circulaire : tu supposes préalablement des électrons
> corpusculaires "plus petits" que l'atome. Tantôt présents, tantôt
> absents, etc. etc. Elles sont où, les expériences qui soutiennent
> cette mystique ?
Je ne suppose rien du tout.
- Afficher le texte des messages précédents -
> > Ca veut dire que la structure
> > des zéros de la fonction d'onde psi(x_1,y_1,z_1,x_2,y_2,z_2) est trés
> > particulière (je te rappelle que la fonction d'onde est fonction des 6
> > coordonnées des deux électrons). A priori il n'y a aucune raison pour que
> > la solution de psi = 0 (où psi est une fonction plus ou moins analytique des
> > x) soit de la forme (x_1,y_1,z_1) appartient à S, (x_2,y_2,z_2) quelconque
> > ou le contraire. Ceci suppose une dégénérescence, une factorisation de psi
> > qui ne peut pas se produire en général.
> La topologie ne subit aucun changement dans les levées de
> dégénérescences des fréquences et niveaux d'énergie. Seuls changent
> les rayons, la répartition azimuthale dans les Z élevés, et
> éventuellement des couplages r-azimuth qui déforment la symétrie
> sphérique vers une tétraèdrique, ou autre dans les molécules et les
> cristaux.
Tout ce baratin est du traîtement perturbatif, totalement irrelevant pour mon argument. Ni rayon ni azimuth ni rien de tout celà n'existe pour un système à deux électrons et à plus forte raison à beaucoup d'électrons. Tu étales ton incompréhension totale du sujet.
> > Au total je maintiens mon argument et je prétends que c'est toi qui doit
> > réfléchir à la situation avant de parler des erreurs grossières des autres.
> Il s'agit toujours d'une erreur grossière, et pour soutenir une thèse
> toujours indéfendable.
Non l'erreur grossière est dans ton camp.
--
Michel TALON
Jacques Lavau, 14 avr 2006, 09.27
Michel Talon a écrit :
- Afficher le texte des messages précédents -
> ... Non l'erreur grossière est dans ton camp.
Nous sommes toujours en train de raisonner sur les solutions de l'équation de Schrödinger, de 1926, établie sur des bases strictement ondulatoires. En 1924, Louis de Broglie n'avait pas encore dépassé le stade de l'optique géométrique, par rayons, appliquée à l'électron ; inapplicable donc en milieu dispersif, où l'équivalent de l'indice de réfraction dépend du potentiel local. Incité par Debye et Einstein, Schrödinger franchit le pas suivant, fournissant l'équation d'onde dans le cas général - spin exclu. Dans un premier temps, Schrödinger commence par écrire l'équation relativiste, connue depuis sous le nom de Klein-Gordon, puis se rabat sur l'équation non-relativiste, qui est restée depuis, et est toujours intensivement utilisée par les chimistes. En parfaite conformité avec son hypothèse ondulatoire, Schrödinger avait décrit que dans le cas des nombres quantiques élevés l'onde changeait de signe en fonction du rayon et de l'azimuth, en passant donc par zéro.
Deux ans plus tard, Dirac établit l'équation relativiste de l'électron. Relisez son paragraphe 67 de son Principles of Quantum Mechanics. Son titre est bien "The *wave* equation of the electron". Et à aucun moment, il ne fait aucune hypothèse corpusculaire.
Là dessus, pour des raisons de concurrence entre personnes pour le
territoire, Schrödinger a été vaincu au congrès Solvay de 1927, par
Heisenberg et Born, après l'avoir été jusqu'à l'épuisement et la maladie,
en décembre 1926 par Niels Bohr à København. D'autres se sont joints aux
vainqueurs. Et sur quoi a-t-il été vaincu ? Sur des arguments qui sont
tous tombés par la suite :
- Dans la mesure où le temps et la causalité microphysique sont de
même nature qu'en macrophysique, et par conséquent où l'on postule
zéro absorbeur, alors ton onde d'électron abandonnée à elle-même se
dilue dans tout l'espace à vitesse foudroyante (un calcul que l'on
recommence en TD de Licence).
Depuis les expériences dirigée par Alain Aspect à l'Institut d'Optique d'Orsay, nous savons tous que ce postulat de causalité microphysique identique à ce qui se passe en macrophysique, est faux. John Cramer depuis au moins 1986, et moi-même depuis 1997 seulement, et d'autres encore, indépendamment, avons conclu que ce postulat "pas d'absorbeur", est faux. Wheeler et Feynman en 1941, avaient aussi obtenu des résultats appréciables, en jetant à la poubelle ce postulat.
Astucieux et positivistes, Ni Born ni Heisenberg n'explicitaient pas pourquoi ils exigeaient une interprétation statistique - et anti-ondulatoire - de l'équation de Schrödinger. Bohr fut plus naïf, et a craché le morceau : pour maintenir la Sainte-dualité et son insondable mystère, et le mystérieux corpuscule néo-newtonien restauré par Einstein en 1905.
Ce que tes contorsions coléreuses révèlent crûment, c'est que depuis que les coucous occupent le nid construit par Schrödinger, ils n'ont encore jamais réussi à construire d'équation de l'atome et des molécules qui soit conforme à leur postulat de "corpuscule" plus petit que l'atome lui-même. Et cela en 78 ans...
Les contradictions entre la sémantique parasite et le cadre
ondulatoire qu'elle occupe, sont légions. Le débat est d'autant plus
passionnel, que les coucous ont un crime collectif sur la conscience :
ils occupent un nid volé.
Si tu veux maintenir ton postulat d'électron corpusculaire, bien plus
petit que l'atome lui-même, et en mouvement farfadique et
inconnaissable, il faut assumer le fardeau qui va avec : la divergence
de la self-énergie.
Chiche ?
Remise en discussion : le statut du pratiquement non observable, mais prédit par la théorie.
Le présupposé implicite de Michel Talon dans la discussion ci-dessus, est que tout ce qui n'est pas "observable", directement observable au sens d'une expérience de labo, peut unilatéralement être déclaré nul et non avenu par une chapelle.
Or la phase, calculée par les équations de Schrödinger, puis de Dirac, et son inversion d'une zone à l'autre, est au nombre de ces inobservables, en pratique, mais que l'on peut confirmer ou infirmer indirectement. Cette chapelle décide donc de jeter la phase, toute la phase, puisqu'elle contredit la sémantique discutable, qui est le ciment de leur chapelle-contre-le-restant-du-monde.
Nous au contraire, nous considérons que le formalisme bien fait, est souvent plus savant que ceux qui s'en servent, voire que ses créateurs. Ici, le formalisme demeure ondulatoire et déterministe, tandis qu'on fait croire le contraire aux étudiants. Jusqu'à preuves expérimentales du contraire, nous persévérons à lui faire confiance, et à tenir en défiance la sémantique nègre-blanc, avec ses "aspects corpusculaires".
C'est un point sérieux, en épistémologie : telle classe d'expériences ne peut ni infirmer ni confirmer la fréquence broglienne, ni les phases dans l'onde électronique stationnaire selon Schrödinger. Le postulat positiviste invoqué par Heisenberg et Born, n'est appliqué qu'à géométrie variable : sont rejetés comme "non-observables" les points qui sont gênants pour leur doctrine, mais eux aussi enseignent des non-observables, qui de plus ont le défaut d'être incompatibles avec le formalisme...
Dans ces conditions, je ne crois en rien que le fait que les solutions pour un atome plus compliqué, soient incalculables, implique que les frontières entre phase + et phase - cessent d'exister. Ou alors, c'est la phase, comme nombre réel à un instant donné, qui est un concept entièrement faux, sauf qu'il n'existe pas le plus petit indice expérimental en ce sens.
Reprise du débat, février 2009
Michel Talon, 3 février 2009
J'ai relu l'enfilade et je ne suis absolument pas convaincu, ni dans un sens ni dans l'autre. En tout cas ce n'est certainement pas élémentaire. Personnellement je n'ai aucune idée si dans un système plus compliqué que le système à un électron, disons pour un atome d'hélium, les zéros de la fonction d'onde forment des surfaces qui décomposent l'espace (*) en composantes connexes. Pour un atome à un électron c'est le cas car le système est intégrable. Et je crois avoir entendu dire que c'était justement une conséquence de l'intégrabilité. C'est un problème purement mathématique, certainement non trivial, et qui n'a rien à voir avec les considération philosophiques sur l'impossibilité supposée d'une particule de passer d'une composante connexe à une autre.
(*) l'espace dans ce cas est un espace à 2 particules, la fonction d'onde est psi(x1,x2) où x1 et x2 sont dans R3, donc l'espace est de dimension 6, et la condition psi=0 représente, je pense, 2 conditions car psi est complexe en général. C'est donc une surface de dimension 4, et je doute qu'elle sépare l'espace en deux. Je crois que l'intuition que tu te fais d'une fonction qui passe par 0 en changeant de signe, est vraie en dimension 1 mais pas nécessairement au delà. En tout cas c'est une question nécessitant réflexion.
Jacques Lavau, 3 février 2009
Débat : l'habitus électronique stationnaire en zones de phases opposées.
1. L'utilité de la solution stationnaire complète pour l'atome
d'hydrogène.
>
Si une théorie se voit opposer un seul contre-exemple valide, alors elle est fausse. La théorie du corpuscule farfadique et divaguant est contradictoire avec les solutions à n > 1, qui comprennent des zones en oppositions de phase, infranchissables par un corpuscule. Dont la sémantique enseignée partout, du "tantôt corpuscule", "aspects corpusculaire", "électron très petit par rapport à l'atome", "l'atome est surtout fait de trou", est fausse. L'atome d'hydrogène suffit, à lui seul, à prouver cette fausseté.
2. Discussion sur la validité de l'extrapolation topologique, pour tous les atomes. Evidemment, tant qu'on oublie qui a construit la maison qu'on occupe depuis qu'on l'a expulsé d'Allemagne puis d'Autriche, tant qu'on oublie la phase pour ne se focaliser que sur le carré hermitien de l'onde, on peut se persuader que les surfaces de changement de phase et donc de densité nulle, cessent d'exister.
Seulement voilà : la justification pour jeter l'onde de Schrödinger, pour ne conserver que son carré hermitien, repose sur le besoin de maintenir le coup du "aspects corpusculaires", via l'entourloupe de la "probablité de présence" du corpuscule... Zéro justification scientifique ; la seule justification est qu'en 1927 cela a permis de classer les physiciens en deux camps : les vainqueurs et les vaincus.
Or à aucun moment dans le calcul formel n'est apparu une phase complexe. Donc toute solution stationnaire à n assez élevé, comprend des zones de phases opposées, avec entre elles des surfaces de densité nulle. Cette caractéristique est purement topologique, et invariante malgré la difficulté de calcul des atomes plus lourds.
3. La vraie objection : les électrons sont interchangeables et indiscernables. Donc si telle zone pour tel électron formellement considéré, est à composantes connexes disjointes, il y a des recouvrements par d'autres zones d'autres électrons. Doit-on considérer que par les autres zones des autres électrons, etc... ? Oui, mais on concilie comment le coup des "aspects corpusculaires" et du "mouvement de l'électron autour du noyau", avec l'échange entre électrons de nombres quantiques distincts ?
Jacques Lavau, 7 février 2009
Personne ne calcule les habitus électroniques des atomes excités.
On calcule seulement les énergies, pour comparaison avec les données expérimentales spectroscopiques.
Le spectre des alcalins est assez étudié pour confirmer que les états excités de l'électron de valence suivent bien le modèle hydrogénoïde.
Cet électron de valence est bien lui aussi, dans les états suffisamment excités, fragmenté en zones de phases opposées, séparées donc par des zones de densité nulle. L'équation d'onde est sans ambiguïté à ce sujet.
On trouve ces spectres dans le tome 2 du Chpolski, Physique Atomique, édition Mir, 1974. 1978 pour la traduction française.
Pour le reste, en atomistique comme en chimie physique, on ne s'intéresse qu'aux états fondamentaux, qui justement ne connaissent pas ces fragmentations en zones et en lobes.
Certes on connaît l'habitus tétraèdrique des électrons de valence du carbone et du silicium, sauf qu'aucun de ces lobes n'est fragmenté à l'état fondamental.
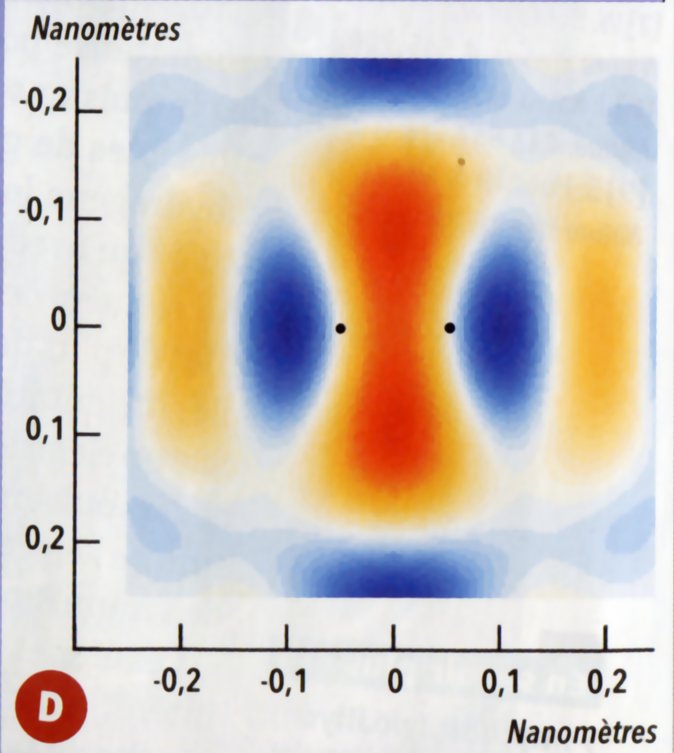
L'expérience a tranché : les domaines de phase des orbitales sont observés
Références :
Itatani et al. Nature 432,867, 2004
S. Haessler et al. Nature, sous presse,
citées par les Dossiers de la Recherche, n° 38, février 2010, pages 63 et 64 : "Des flashes toujours plus courts".
La figure n° 2, présente page 63 porte sur une molécule de diazote dans un état excité, et montre les domaines de phase positive et de phase négative des électrons les plus externes dans la molécule.
Bien sûr, le message est submergé par les baratins habituels en "probabilité de présence", sans lesquels les auteurs seraient exclus du club.
Mais c'est trop tard : l'objection de Michel Talon selon laquelle les domaines de phase opposés, bien calculés dans le cas de l'atome d'hydrogène, n'existeraient plus pour les atomes ou molécules plus compliqués, sous prétexte que le truc n'est plus intégrable, est démentie. Il n'avait pas saisi qu'on ne passe d'une phase + à une phase - qu'en franchissant une frontière à densité électronique identiquement nulle, que ces contraintes topologiques sont indépendantes du caractère intégrable ou non des équations.
En conclusion, c'est bien feu Erwin Schrödinger qui avait raison face à ses vainqueurs de l'époque : l'équation de Schrödinger décrit directement la densité électronique, de l'onde électronique, et non pas la complication inextricable en "probabilité d'apparitions de corpuscule farfadique".
Références :
http://tel.archives-ouvertes.fr/docs/00/44/01/90/PDF/thesis_DrStefanHaessler.pdf ,
http://iramis.cea.fr/spam/MEC/ast_visu.php?num=101&keyw=Atto%20Physique&lang=fr ,
http://iramis.cea.fr/spam/Phocea/Vie_des_labos/Ast/ast.php?t=fait_marquant&id_ast=1550 ,
http://iramis.cea.fr/Phocea/file.php?file=Ast/1550/CP-Photographie_electron__3_-vCNRS.pdf ,
Orbitale HOMO de la molécule d’azote N2, a) calculée exactement (Hartree-Fock), b) reconstruite expérimentalement par la technique tomographique (recollision du paquet d’ondes électronique en champ laser), c) reconstruite théoriquement dans les conditions de b). L’orbitale reconstruite b) présente la structure caractéristique, en amplitude et en signe, de la HOMO exacte.
http://iramis.cea.fr/Images/astImg/1550_4.jpg
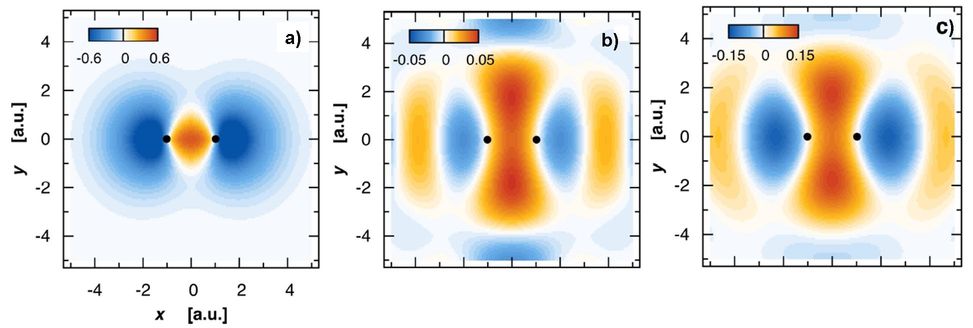
Crédit : Nature Physics.
Auteurs :
S. Haessler, J. Caillat, W. Boutu, C. Giovanetti-Teixeira, T. Ruchon, T. Auguste, Z. Diveki, P. Breger, A. Maquet, B. Carré, R. Taïeb & P. Salières,
Ce que la légende de la communication résumée ne dit pas, mais qui est visible, c'est que la figure de gauche, a), est pour l'état fondamental, et que la figure expérimentale et le calcul de confirmation sont pour un état excité, à plus haute énergie, donc avec des changement spatiaux de phase.