Métrique des grandeurs vectorielles en physique
Prérequis :
Les grandeurs physiques
Vecteurs, définition, propriétés
Sommaire
Module d'un vecteur. Contracté du produit intérieur, ou produit scalaire
Module d'un vecteur
Définition
Le "module" (ou "norme", ou "longueur" chez E. Cartan), généralise la longueur, pour toutes les sortes de vecteurs. Pour un vecteur de déplacement, dans l'espace euclidien de notre expérience courante, ce module est exactement la longueur du bipoint, mesurée avec un double-décimètre.
Le module exprime ce qui est invariant envers l'orientation par rapport aux axes de coordonnées.
Plus généralement, le module satisfait aux trois axiomes des normes:
pour tout
réel (ce qui implique :
= 0).
, inégalité triangulaire.
Ces deux premiers axiomes sont aussi remplis par les pseudo-normes, des espaces pseudo-euclidiens, tels l'espace de Minkowski. L'axiome suivant est caractéristique des vraies normes :
pour tout vecteur non nul.
La physique exige de plus que l'expression analytique de ce module, donne un résultat intrinsèque indépendant du choix des coordonnées, et des unités. Un résultat invariant, ni covariant, ni contravariant,INVARIANT. Le module d'un vecteur physique n'est donc pas un simple nombre, mais est une grandeur physique. Il a donc une unité physique, par exemple des mètres. Pendant très longtemps, les conséquences de cette exigence basique n'ont pas été perçues.
Calcul du module d'un vecteur
Calcul en dimension 1 : le long d'une droite.
Il nous suffit de savoir le module du vecteur unité, , car
= v.
, donc
.
Si on change d'unité, par exemple en prenant 100 fois plus petit, la coordonnée v devient 100 fois plus grande, pour maintenir l'invariance de ce qui est représenté, envers le mode de représentation.
Calcul en dimension 2 : sur un plan.
Cas ultra-simplifié: le repère est orthonormal.
Autrement dit , et ces deux vecteurs sont perpendiculaires.
On peut alors utiliser le théorème de Pythagore, sans précautions.
On exprime ces coordonnées en fonction de l'angle du vecteur V avec les axes, par son module multipliant les sinus et cosinus. Or l'exigence d'invariance du résultat envers ces angles avec le repère n'est satisfaisable que par la somme du carré du cosinus et du carré du sinus. Il en résulte au final que :
Cas moins simple: le repère est orthogonal.
Les deux vecteurs et
sont perpendiculaires, mais leurs modules ne sont pas égaux.
Ce cas est courant sur les cartes de géographie, ou pour le repérage d'un avion en vol : les distances au sol sont en kilomètres, et l'altitude est en mètres.
Résultat final :
Cas général en base quelconque ?
Il faudra aussi tenir compte des angles entre eux des vecteurs de la base, donc construire explicitement le tenseur métrique de cette base. Nous y reviendrons.
Calcul en dimension 3 et plus : sur un l'espace ordinaire, l'espace-temps de Minkowski, etc.
Rien de nouveau : on ajoute un troisième terme en dimension 3, un quatrième terme en dimension 4, etc.
Par exemple en repère orthogonal, en dimension 3 :
Le produit scalaire de deux vecteurs (produit intérieur, contracté).
Définition.
Pour tenir la route, la définition doit être donnée en grandeurs physiques, en non en coordonnées. En effet, les coordonnées n'ont de signification qu'à partir des propriétés des vecteurs de base.
, où
désigne la longueur, ou le module, du vecteur
Cette définition est intrinsèque, et découle de la projection intérieure.
Au temps où l'on confondait allègrement les grandeurs physiques avec les nombres, on prenait le "produit scalaire" pour un nombre, et c'était la source de confusions et de mésaventures sans fin. Evidemment, un nombre multiplié par le carré d'une longueur, n'est pas un nombre, mais une grandeur scalable, de dimension homogène à une aire.
Usages
En physique, le produit scalaire (produit intérieur, contracté), sert surtout à calculer le travail d'une force :
force x déplacement x cosinus (force; déplacement).
Autrement dit, avant de multiplier la force par le déplacement, on commence par projeter l'un sur l'autre, et
la projection est orthogonale. C'est bien la projection intérieure qui est utilisée ici. Puis on prend le
produit des modules.
En géométrie, le produit intérieur, contracté, sert à calculer des angles, et des longueurs. Il est donc à la base de toutes les relations métriques de la cristallographie.
Piège
Pour que le produit scalaire soit un nombre, un vrai nombre, il faut qu'un vecteur soit en mètres, et l'autre en m-1. Autrement dit, seul le produit scalaire d'un vecteur par un covecteur (ou l'inverse, puisque ce produit est commutatif), peut donner un nombre.
Propriétés du produit scalaire (produit intérieur, contracté)
Elles découlent de la définition.
Ce produit conserve évidemment la multiplication par un nombre:
Il conserve aussi l'addition, donc la projection et la décomposition en projections sur les axes de
coordonnées. Cela se déduit de la linéarité de l'opérateur de projection: la projection sur un axe, de la
somme de deux vecteurs, est la somme des projections de ces vecteurs sur le même axe. On en conclut que
le produit scalaire est distributif sur les opérations de somme vectorielle, et de multiplication par un
nombre.
La contraction brise l'associativité, qui était conservée et par le produit tensoriel, et par la symétrisation. Le produit scalaire n'est pas associatif.
Expression du produit scalaire avec les coordonnées.
Soient ,
,
, les trois vecteurs de base. Les longueurs j, k, l, sont les modules de ces vecteurs
,
,
. Les angles (
,
), (
,
), (
,
) sont notés
,
,
.
Expression simplifiée, en repère orthonormé
Les angles ,
,
sont supposés droits, donc leurs cosinus sont tous nuls. Donc les produits scalaires suivants sont nuls :
,
,
,
,
,
.
Les trois autres sont unitaires par hypothèse : = j² = unité au carré.
= k² = unité au carré.
= l² = unité au carré.
On utilise alors la distributivité :
=
.
En effet, les termes croisés sont tous affectés de coefficients nuls.
D'où unité².
Expression complète avec les coordonnées
Pour l'expression générale, on est amenés à calculer, pour chaque système de vecteurs de base, un tableau carré g, où sont portés les produits scalaires de chaque vecteur de base, par chaque vecteur de base.
Cela s'appelle le tenseur métrique, ou plus anciennement, la matrice de Gram (au sens des mathématiciens, en oubliant l'unité physique). Une base est orthonormale, si et seulement si sa matrice de Gram est la matrice unité multipliant le carré de l'unité de longueur. De toute évidence, g est un tenseur symétrique, et il est deux fois covariant, par construction.
D'où le carré du module d'un vecteur, comme produit contracté, dans le cas général :
Sans le tenseur métrique vous ne pourriez rien faire en cristallographie et radiocristallographie : angles de droites, angles de droites et plans, angles de plans, distances entre plans, etc. Avec le tenseur métrique et les six paramètres de maille vous pouvez prédire toutes les raies d'un diffractogramme X (ou électronique, ou neutronique); vous en prédisez même trop, car selon le remplissage par le motif de maille, certaines raies sont nécessairement éteintes.
Cette relation s'étend au produit scalaire de deux vecteurs :
Ce nom de "tenseur" est encore un de ces hasards cocasses de l'Histoire. Il se trouve que le premier physicien à s'emparer des outils de "calcul différentiel absolu" de Gregorio Ricci-Curbastro et de Tullio Levi-Civita, fut Woldemar Voigt, qui en avait l'usage pour décrire l'élasticité des cristaux.
Par un hasard similaire, un chant guerrier composé à Strasbourg pour l'armée du Rhin, devint ensuite "la Marseillaise". Il n'y a aucune espèce de "tension" à interpréter dans "tenseur", ni rien de marseillais dans notre hymne national. Il n'y a là rien de plus que le premier utilisateur qui ait été vraiment remarqué.
Changements de base
Expression matricielle des changements de base
Cette expression découle directement de la définition des vecteurs comme classes d'équivalence des bipoints. Elle généralise ce que nous avons vu de la covariance et de la contravariance, rappelé dans l'article précédent. Ecrivons les coordonnées des nouveaux vecteurs de base, selon l'ancienne base :
et
, puis assemblons ces colonnes de coordonnées en un tableau carré, appelé matrice de changement de base :
en dimension 2, et
en dimension 3.
Que notre espace vectoriel soit de dimension 2, 3, 4 ou 77, le principe est le même.
Nous pouvons calculer la matrice inverse T-1, telle que T-1.T = T.T-1 = 1.
T-1 est la matrice qui exprime l'ancienne base en fonction de la nouvelle. Nous avons déjà vu que les coordonnées d'un vecteur sont contravariantes à la base : un vecteur est du genre longueur. On pourrait le dire en style plus savant, mais cela n'apporterait rien de plus. Donc c'est la matrice T-1 qui transforme les anciennes coordonnées d'un vecteur dans les nouvelles (le même vecteur, exprimé selon la nouvelle base) :
Soit un vecteur quelconque, exprimé dans l'ancienne et la nouvelle base (dimension 3 ou n, qu'importe) :
A partir de cet instant, on s'imposera la discipline de n'écrire les coordonnées contravariantes qu'avec des indices en haut. Il faudra ne pas confondre avec l'écriture des puissances d'un nombre.
A. Einstein (1879-1955) a condensé cette écriture, par la convention que tout indice répété en haut et en bas, signifie une sommation sur cet indice. Réécrivons selon la convention d'Einstein :
Or, par définition de T, . Donc
. On peut validement simplifier par les vecteurs de base.
Il vient : . C'est à dire les anciennes coordonnées en fonction des nouvelles. Nommons
les coordonnées de la matrice inverse T-1. On peut alors exprimer les nouvelles coordonnées en fonction des anciennes :
.
Les covecteurs ont le comportement dimensionnel opposé, soit exactement celui des vecteurs de la base : la matrice T change les anciennes coordonnées en les nouvelles.
Tels sont le comportement dimensionnel des vecteurs, et celui des covecteurs. Ce comportement est caractéristique, et ne connaît aucune exception. Si les coordonnées d'une grandeur ont un autre comportement envers un changement de base que celui d'un vecteur (respectivement : d'un covecteur), alors elle n'est pas un vecteur (resp. : un covecteur).
Cette règle est consubstantielle à la physique macroscopique.
Garde-fou dimensionnel
Reprenons l'exemple d'un vecteur de l'espace affine ordinaire :
= Vj
+ Vk
+ Vl
. Il est naturellement rapporté à des vecteurs unitaires de base, qui sont eux-mêmes rapportés à une unité de longueur. Ces vecteurs unitaires sont donc exprimés en mètres. Tandis que les coordonnées (contravariantes) de notre vecteur sur ce repère, ne sont que des nombres.
Les composantes du tenseur métrique g, sont donc exprimées en mètres carrés, leur unité naturelle. Les composantes du tenseur métrique réciproque sont donc en m-2. Le covecteur inverse de s'exprime naturellement sur la base duale (contravariante), qui est en m-1 :
.
= 1.
Il est devenu habituel de considérer sans précautions une seconde expression possible : exprimer en fonction de la base duale, et inversement, le vecteur dual en fonction de la base directe. Mais alors les nouvelles coordonnées cessent aussitôt d'être des nombres sans dimension.
Sur la base duale (contravariante, en m-1), les coordonnées (covariantes) de sont en m2. Si l'on passe en unités cm, les coordonnées sont alors divisées par 100 : ce sont des cm2. Tandis que les coordonnées naturelles (contravariantes) sont multipliées par 100.
Résumons : 2 m = 2 x 1 m = 200 x 1 cm = 200 cm2 x 1 cm-1 = 2 m2 x 1 m-1.
Nous avons bien vérifié sur les coordonnées covariantes : 200 cm2 = 2 m2 /100.
Sur la base directe (en m), les coordonnées du dual de sont en m-2. Si l'on passe en unités cm, les coordonnées sont alors multipliées par 100. Tandis que les coordonnées naturelles sont divisées par 100.
Résumons : 0,5 m-1 = 0,5 1 m-1 = 0,005 1 cm-1 = 0,005 cm-2 1 cm = 0,5 m-2 1 m.
Nous avons bien vérifié sur les coordonnées contravariantes : 0,005 cm-2 = 0,5 m-2x 100.
Et pourtant, depuis Elie Cartan, tout le monde croyait malin de répéter cet énorme barbarisme dimensionnel : "En repère orthogonal, la distinction entre composantes covariantes, et composantes contravariantes disparaît". Autrement dit : 200 = 200 cm2. Et 5 = 5 cm-2. Ahurissant. Tout est prêt pour l'affirmation : "5 flacons = 5 pétroliers", ou pour le calcul de l'âge du capitaine en additionnant les chèvres avec les oies.
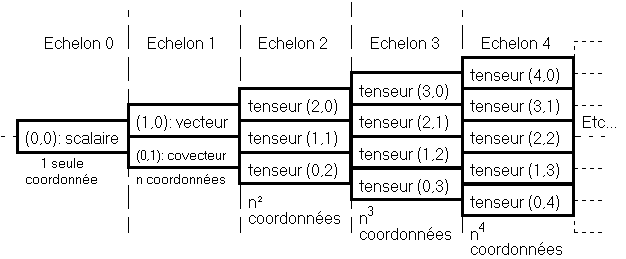
Livret de famille des grandeurs géométriques de la physique sur un espace vectoriel (de dimension n)
Si le comportement des coordonnées d'une grandeur, ressemble à celui des coordonnées d'un vecteur ou d'un covecteur, en ce sens qu'il faut appliquer n fois la matrice de changement de base, et p fois la matrice inverse, alors cette grandeur appartient à la famille plus générale des tenseurs, ici n fois covariant, p fois contravariant, ce qui se note : de type (p, n).
Nous venons de citer le tenseur métrique, sous la forme de type (0,2) : coordonnées 2 fois covariantes.
Avant éventuelle contraction, le produit d'un vecteur par un covecteur, est de type (1, 1). Le produit de deux vecteurs est de type (2, 0). Le produit de deux covecteurs est de type (0, 2). La contraction d'un type (1, 1) a pour résultat un type (0, 0), scalaire. Sur un espace vectoriel de dimension n, un tenseur d'ordre p, a exactement np coordonnées. Mais des conditions de symétrie peuvent en restreindre l'indépendance.
Plus généralement, le dual (au sens algébrique, seul cohérent) d'une grandeur physique, a toujours les mêmes propriétés de symétrie. Pour l'instant, nous ne l'avons constaté que pour les vecteurs et leurs duaux, les covecteurs. Nous verrons ensuite le lien étroit avec la dimension physique, et avec le théorème de Noether.
Références
Suite : Les quart-de-tours entre vecteurs : gyreurs
Pour aller plus loin : Lemmes pour l'algèbre des tourneurs : http://jacques.lavau.perso.sfr.fr/syntaxe3.htm